The Solar angles: An important factor for improving the power conversion efficiency
Introduction
A solar energy is one of the most prominent renewable energy source in India. The solar panel’s output efficiency at max is ~22% and it heavily depends upon various internal and external factors. To begin with, solar angles are one of the crucial external factors to be considered while installing the PV panel on any roof. Hence, In this article, our main focus will be on these different types of solar angles.
Azimuth angle
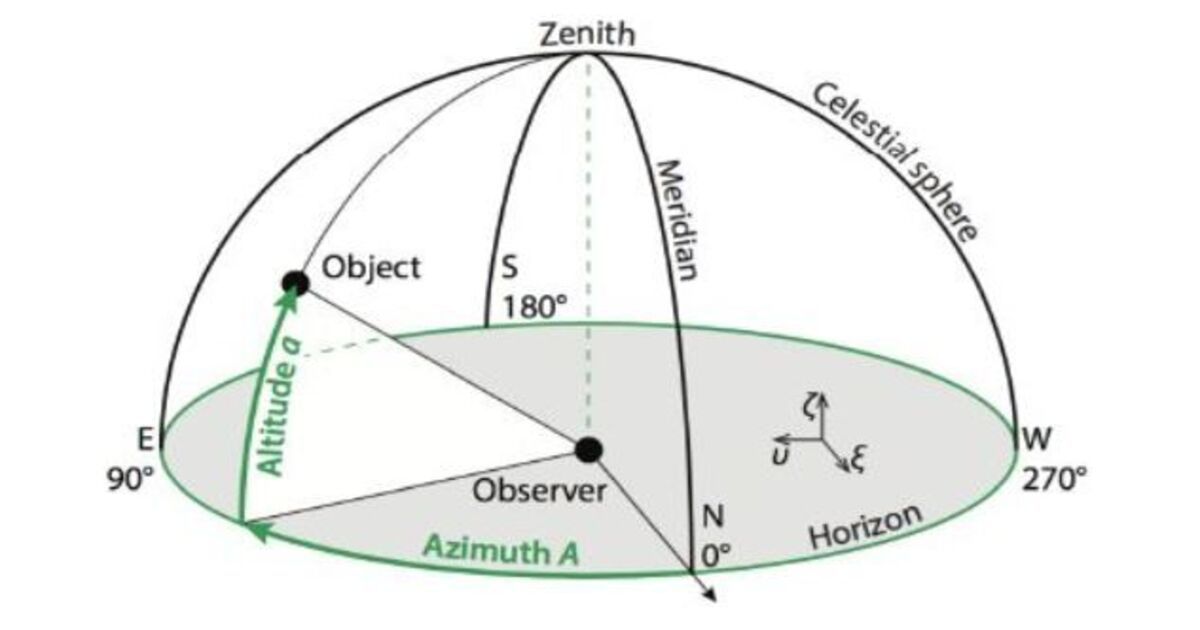
As we all know heaven’s objects such as the Sun, the Moon and the stars are far away from the Earth. Therefore, to simplify the motion measurements of these objects, the imaginary sphere is used, which contains an arbitrary radius and it is concentric towards the Earth. Coming back to the azimuth angle, it is calculated by measuring the angle between North 0 and the altitude angle. Besides, the altitude angle [a] is nothing but the angular elevation of the object above the observer’s horizon. the range of angular elevation varies from [-90 to 90 degrees], where -90 stands for the object being below the horizon and thus not visible. In this case, the observer’s horizon can also be called the fundamental plane. on the other hand, the azimuth angle can be calculated in 4 main constituents, such as A= 0, 90, 180, 270 degrees which correspond respectively to North, East, South, and West.

Zenith angle
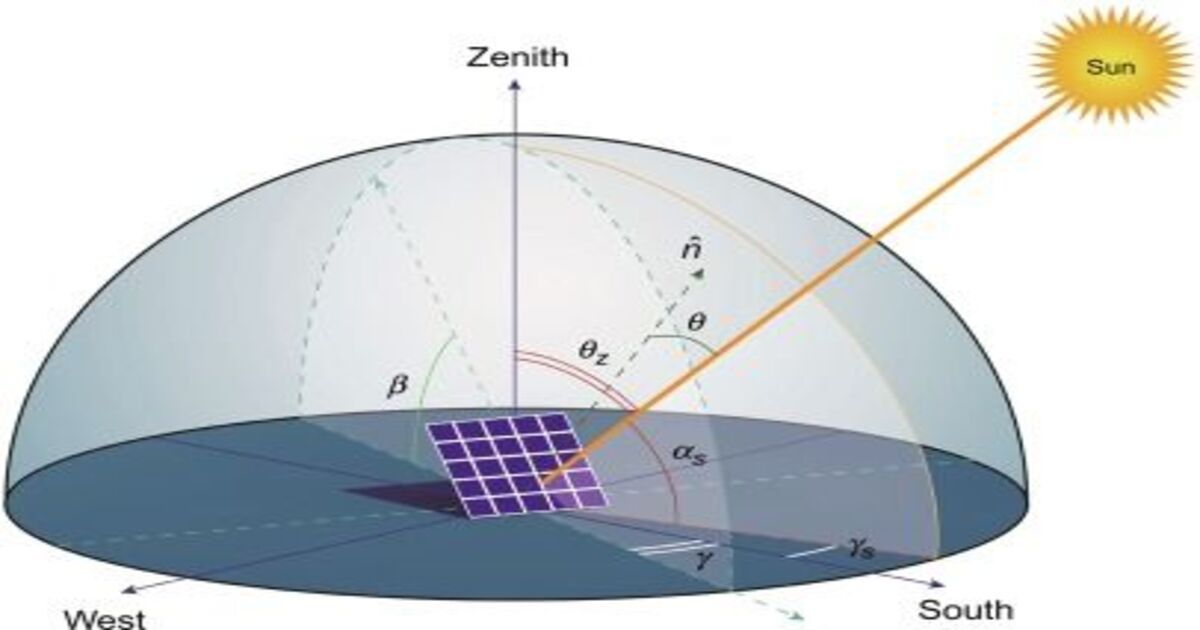
Zenith in astronomy terms means the point in sky which is exactly above you, no matter wherever you stand on the Earth. Keeping that in mind, the zenith angle becomes an angle between the zenith and the Sun. It works complementary with the elevation angle, in which angular motion is calculated between the horizon and the Sun. As mentioned earlier these two angles work in a complementary manner, hence cosine of the one equals the sine of the other.
Zenith angle can be calculated as:
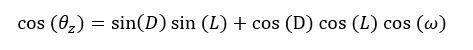


Hour angle
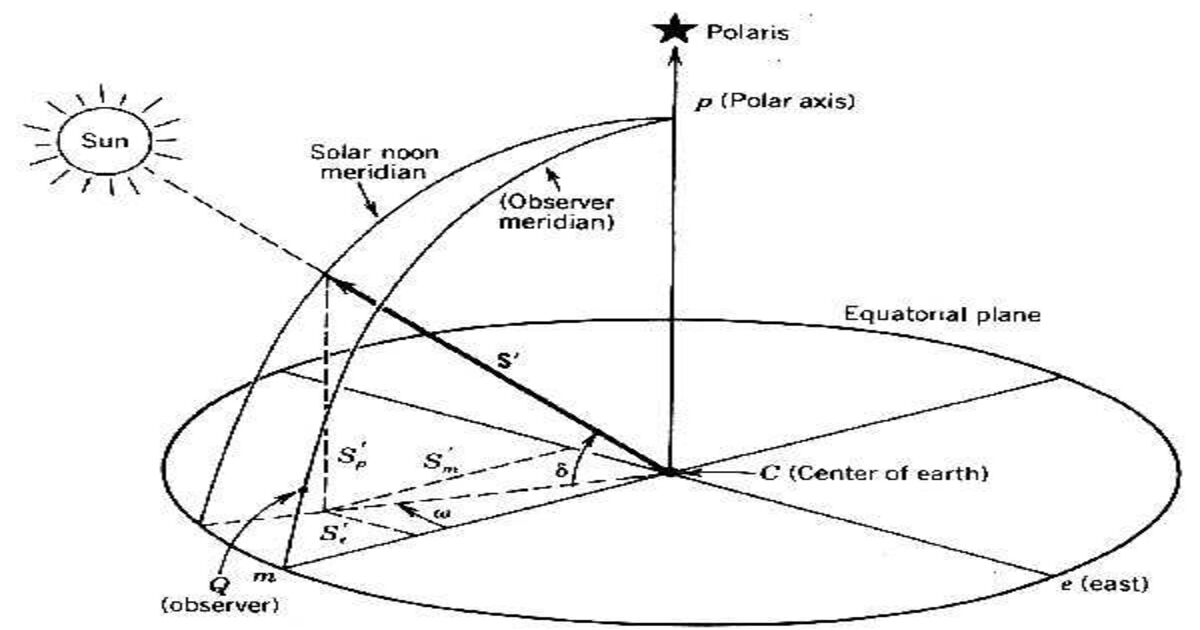
The hour angle is the angular distance between the line of longitude (also known as the meridian) of the observer and the line of longitude which contains the Sun. Besides, the hour angle becomes zero at noon. Also, whenever the observers longitudinal plane contains the Sun, the hour angle increases by 15 for every hour.
The hour angle can be calculated as:
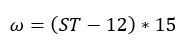
(It varies from -ve before the solar noon to +ve after the solar noon)
For Example:

Declination angle
It is the angle made between the ray of the Sun, extended to the centre of the Earth, and the equatorial plane of the Earth.
Whenever the rays of Sun reaches to the centre of the Earth via Northern hemisphere, the declination angle becomes positive and whenever it reaches from the Southern hemisphere, it becomes negative.
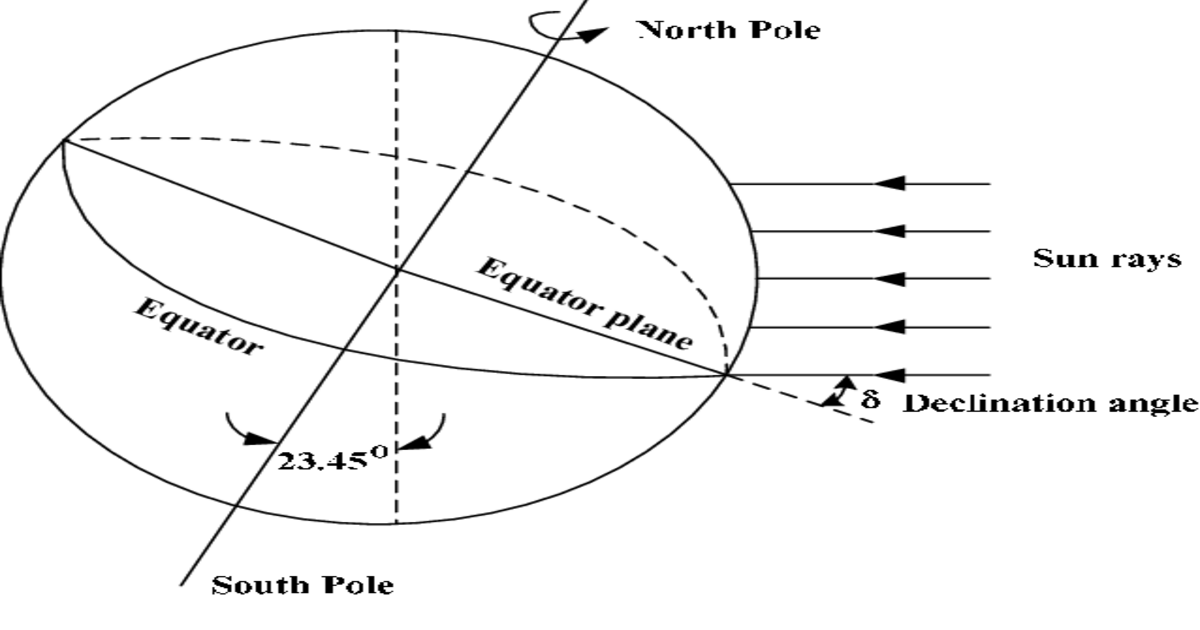
In the summer solstice, the value of solar declination angle is marked as
+23.5 degrees and during the winter solstice, it is marked as -23.5 degrees
. Hence the solar declination angle varies from -23.5 < d <
23.5 degrees.
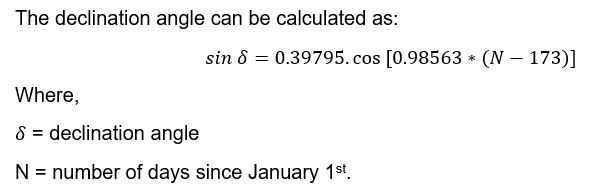
Altitude angle
The solar altitude angle is the angular distance between the rays of Sun and the horizon of the Earth. The solar altitude angle varies because of the three main factors which are, the time of the day, the time of the year, and the latitude of the Earth respectively.
The altitude angle can be calculated as:

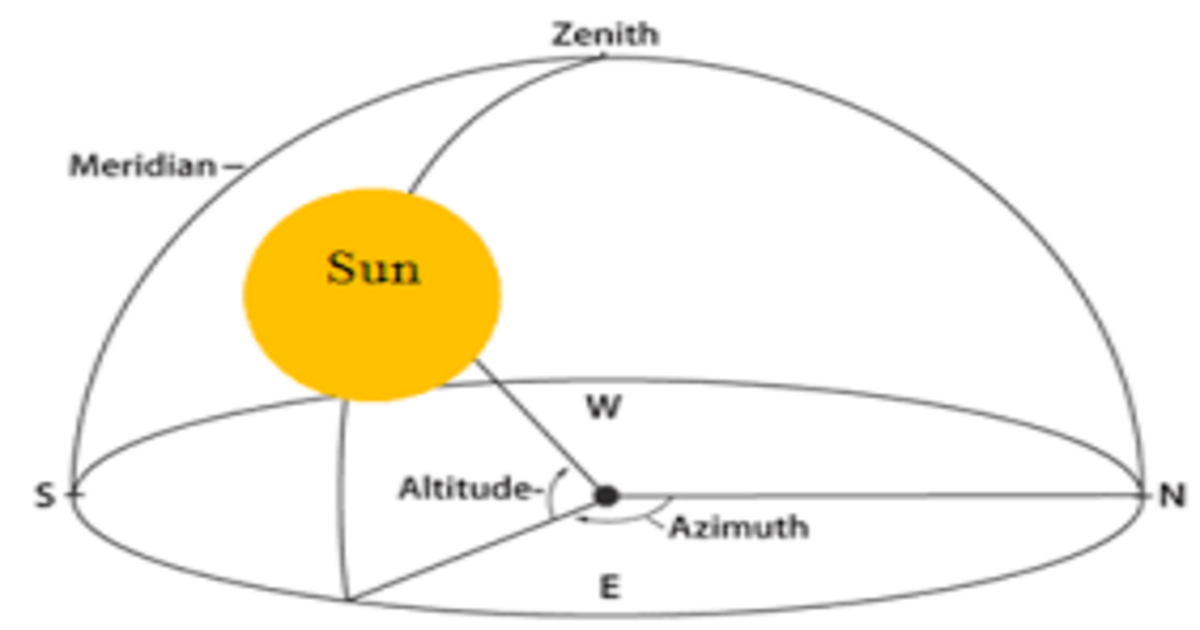
Incidence angle
With respect to solar energy systems: the angle of the sun’s ray renders a line perpendicular to the earth; for example, the earth directly facing the sun has an angle of zero incidence, and the surface parallel to the sun (such as a sunrise reaching a horizontal rooftop) has an angle of 90 °. Sunlight at 90 ° angle of incident tends to be absorbed, while lower angles tend to be reflected.
Incidence angle can be calculated as:

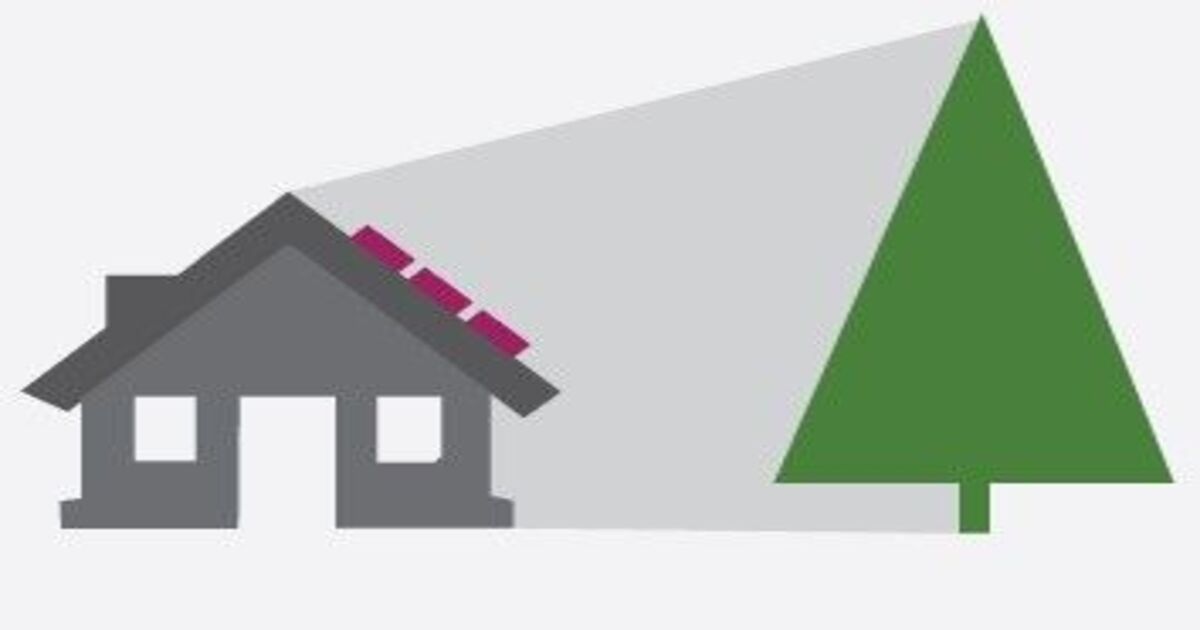
Shadowing
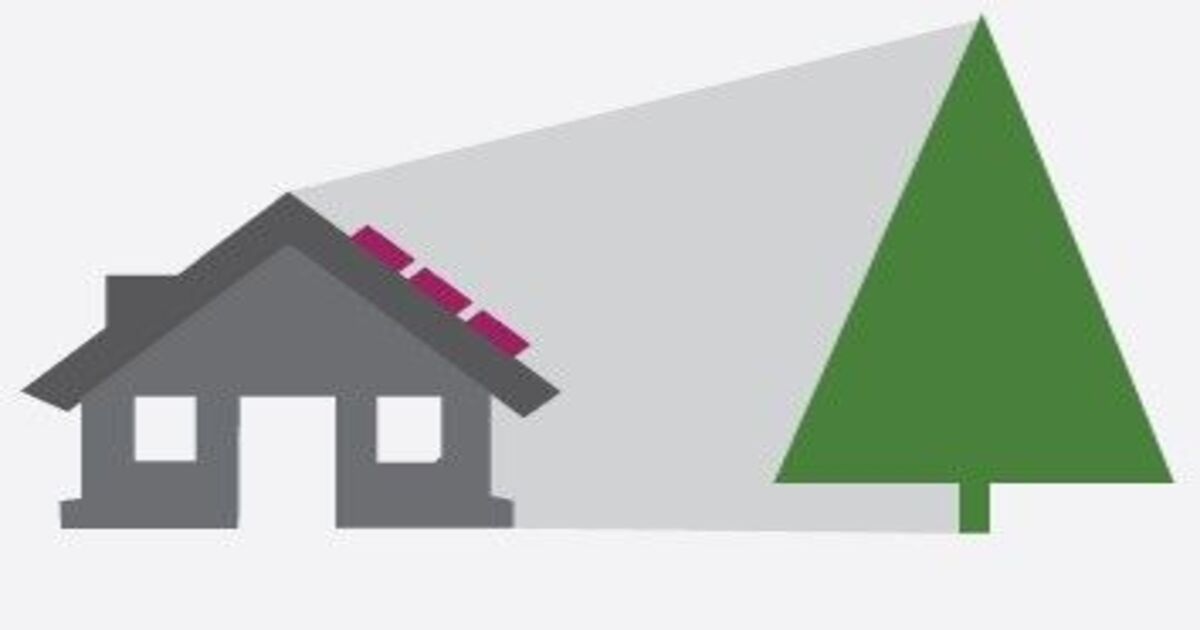
While installing the solar panels on the roof or the facade, the shadowing factor plays a crucial role. It is the shadow projected by the surrounding objects on the panel. Besides, it is necessary to be aware of the shadow cast, as it changes daily.
The shadowing factor can be regulated by a “solar profile angle” and it can be calculated as:

Conclusion
In conclusion, to enhance this investigation and decrease possible errors, a number of angles must have been done. There might be a stand that is set at the right angle. That would make the angle accurate and not a few degrees off, which could interrupt the collection of energy. There could also only be experiments on clear days with almost no clouds to prevent clouds from changing the results to enhance the experiment. There could be multiple solar panels set at different angles to further analyse what angle of a solar panel would work best. The solar panels would then be left out all day and then see which angle, after 24 hours, gathered the greatest amount of energy.

